RAPPORT D'AVANCEMENT No 2 ANALYSE SYNTAXIQUE ET SEMANTIQUE RT EMP 105

RAPPORT D'AVANCEMENT No 2
ANALYSE SYNTAXIQUE ET SEMANTIQUE
RT EMP 105

François IRIGOIN

Pierre JOUVELOT

Mars 1988

Rémi TRIOLET

Introduction

Ce rapport intermédiaire est consacré à la description de la représentation intermédiaire que nous avons choisie pour stocker les programmes scientifiques qui seront soumis à PIPS. Rappelons que ces programmes sont écrits dans un sous-ensemble du langage Fortran que nous avons défini dans un précédant rapport¹.

Tout programme Fortran doit avoir une représentation intermédiaire sémantiquement équivalente à son texte Fortran.

Cette représentation intermédiaire doit permettre d'effectuer facilement des transformations et des analyses de programmes.

Le développement de PIPS est en partie basé sur un outil de génie logiciel que nous avons développé au CAII. Cet outil s'appelle NewGen, il est présenté dans la première partie de ce rapport.

La représentation intermédiaire est décrite dans la seconde partie. Nous expliquons notamment comment un programme Fortran est mappé sur cette représentation intermédiaire.

La troisième partie de ce rapport est consacrée à l'analyse sémantique. Nous y présentons d'abord les objets utilisés pour résoudre les équations aux polyèdres propres à la méthode de Cousot et Halbwachs, puis la structure de données représentant un tel système d'équations pour un module quelconque.

Présentation de NewGen

Introduction

NewGen est un outil de génie logiciel développé au CAII pour faciliter l'écriture de gros logiciels tels que PIPS. NewGen est dérivé de deux outils antérieurs, dont il est une amélioration:

GenPgm, développé au CAII par Rémi Triolet,
MetaGen, développé au groupe Bull par Pierre Jouvelot.

NewGen facilite à la fois la définition et l'implémentation des structures de données qui sont généralement utilisées pour réaliser des logiciels complexes. L'utilisation de Newgen se fait de la façon suivante.

les types de données que l'on souhaite utiliser pour développer un logiciel (par exemple PIPS) sont définies à l'aide d'un langage de haut niveau appelé ``langage de définition de domaines''.
la définition des domaines est compilée par NewGen, ce qui a pour effet de:
- générer une implémentation des types de données en langage C ou en langage Lisp;
- générer des fonctions de création, destruction et mise à jour d'objets de ces types;
- générer des fonctions d'écriture et de lecture d'objets de ces types sur fichiers.

Le logiciel peut ensuite être développé en tirant profit des fonctions et définitions de types qui ont été générées automatiquement. Les répercussions sur le développement sont nombreuses.

Un langage plus riche

Quel que soit le langage de développement utilisé (Lisp ou C), NewGen l'enrichit de nouvelles constructions: les fonctions de création, destruction et mise à jour d'objets.

Cet enrichissement a plusieurs conséquences. Tout d'abord, tous les membres d'une équipe de développement utilisent les mêmes fonctions et les mêmes types de données, ce qui a pour effet d'uniformiser la façon de programmer. Ensuite, la disponibilité de ces fonctions permet à chacun de programmer plus vite, de comprendre plus facilement le code des autres, et de diminuer la quantité de commentaires nécessaires.

Vérification dynamique de types

Les fonctions de création, destruction et mise à jour d'objets sont créées par NewGen de telle sorte qu'une vérification dynamique soit effectuée. Par exemple, un appel à la fonction employe_nom sur un objet e vérifie d'abord que e est un objet de type employe, si oui renvoie le nom de cet employé et si non aborte avec un message d'erreur. Bien évidemment, cette vérification dynamique est optionnelle, de sorte que les programmes corrects ne sont pas ralentis.

Communications inter-passes par fichiers

Les fonctions d'entrées-sorties générées par NewGen permettent d'écrire ou de lire sur fichier un objet aussi compliqué qu'une représentation intermédiaire de programme Fortran, à l'aide d'une ligne de C ou de Lisp. Ceci a plusieurs conséquences.

Les gros logiciels tels que PIPS sont généralement constitués de plusieurs passes. Il y a des dépendances entre passes, par exemple quand une passe utilise les résultats d'une autre passe. Certaines passes sont obligatoires, d'autres sont optionnelles (comme par exemple la phase d'optimisation dans les compilateurs).

L'organisation généralement adoptée est celle où chaque passe est une procédure appelée par un ``driver'' que l'utilisateur commande soit de façon interactive soit par des lignes de contrôle dans le programme source, ou bien encore par des options de lancement.

L'organisation choisie pour PIPS est radicalement différente. Grâce à NewGen nous avons la possibilité de rendre chaque passe indépendante: chaque passe lit un ou plusieurs fichiers de données à l'aide des fonctions NewGen, effectue ses calculs, puis produit à son tour un fichier résultat. Les données stockées sur un fichier peuvent être arbitrairement complexes (structures, tableaux, listes, graphes) car les fonctions générées par NewGen prennent en compte ce genre de données. Le driver n'est alors plus nécessaire, quelques script-shells suffisent.

Avec une telle organisation, le développement est considérablement simplifié, car on est amené à développer N petits logiciels plutôt qu'un unique gros. La mise au point est plus simple, les temps de compilation plus courts, le partage du travail facilité. Enfin, il est très facile d'utiliser plus d'un langage de programmation car un fichier de données écrit par une passe C peut être lu par une passe Lisp, et ce sans aucune modification du fichier ou des passes.

Définition des domaines NewGen

Les types de données NewGen sont appelés des domaines, et la spécification d'une structure de données NewGen est constituée d'une liste de définitions de domaines. Les définitions de données peuvent être récursives (ou cycliques), c'est à dire qu'un domaine peut être défini en fonction de lui-même, directement ou indirectement.

Les domaines sont définis à partir de deux constructeurs, l'union + et le produit x, de deux itérateurs, le tableau [] et la liste *, et enfin de domaines prédéfinis qui correspondent à peu près aux types simples de C ou Lisp.

A chaque domaine correspond un ensemble de valeurs qui sont les valeurs que peut prendre un objet de ce domaine. Ainsi, les valeurs du domaine prédéfini int sont les entiers relatifs de $\cal Z$ .

Nous allons définir constructeurs et itérateurs en fonction de ces ensembles de valeurs.

Le produit

Un domaine D est le produit de n domaines SD1, SD2, ..., SDn si D est défini par:

D = SD1 x SD2 x ... x SDn ;

Les SDi sont appelés les sous-domaines de D. Un sous-domaine peut être un sous-domaine de base, un sous-domaine simple, un sous-domaine liste ou un sous-domaine tableau (voir plus loin).

L'ensemble des valeurs de D est le produit cartésien des ensembles de valeurs des sous-domaines SDi.

L'union

Un domaine D est l'union de n domaines SD1, SD2,..., SDn si D est défini par:

D = SD1 + SD2 + ... + SDn ;

De même, les SDi sont appelés les sous-domaines de D.

L'ensemble des valeurs de D est l'union des ensembles de valeurs des sous-domaines SDi.

Sous-domaines de base

Un sous-domaine de base est de la forme:

nom:dpd

où nom est le nom du sous-domaine et dpd est un domaine pré-défini: unit , bool , char , string , int et float.

L'ensemble des valeurs d'un sous-domaine de base est égal à l'ensemble des valeurs du domaine pré-défini. Les types pré-définis autres que unit ont des ensembles de valeurs qui dépendent du langage utilisé. Par exemple, le sous-domaine float correspond aux nombres réels.

Le type pré-défini unit a un ensemble de valeurs réduit à un élément, conventionnellement noté constructeur +, dans le cas où le nom du sous-domaine à lui seul porte toute l'information utile.

Exemples:

employe = nom:string x age:int x salaire:float
complex = i:float x r:float
projet = pips:unit + vast:unit + paf:unit

Sous-domaine simple

Un sous-domaine simple est de la forme:

nom:dom

où nom est le nom du sous-domaine et dom le nom d'un domaine construit par + ou x, dont la définition doit se trouver dans le même fichier de spécifications (les références en avant sont admises) ou doit être importée depuis un autre fichier par la commande import. Il est possible d'écrire nom à la place de nom:nom.

L'ensemble des valeurs du sous-domaine nom est égal à l'ensemble des valeurs du domaine dom.

Dans les exemples suivants, annee, mois, naissance, ... sont des sous-domaines simples.

date = annee:int x mois:int x jour:int
employe = nom:string x naissance:date x salaire:float

import expression from "expression.spec"
dimension = lower:expression x upper:expression

Sous-domaine liste

Un sous-domaine liste est de la forme:

nom:dom*

où nom:dom est un sous-domaine de base ou un sous-domaine simple.

L'ensemble des valeurs du sous-domaine nom est égal aux listes à zéro ou plus éléments dont chaque élément à une valeur dans l'ensemble des valeurs du domaine dom.

Dans les exemples suivants, args et block sont des sous-domaines listes.

call = function:entity x args:expression*
instruction = block:statement* + loop:loop + ...

Sous-domaine tableau

Un sous-domaine tableau est de la forme:

nom:dom[d1][d2]...[dl]

où nom:dom est un sous-domaine de base ou un sous-domaine simple et d1, d2, ..., dl sont l constantes entières.

L'ensemble des valeurs du sous-domaine nom est égal aux tableaux à l dimensions d1, d2, ..., dl d'éléments. Chaque élément du tableau ayant une valeur dans l'ensemble des valeurs du domaine dom.

Exemple: La représentation intermédiaire de PIPS

Les deux constructeurs + et x, les deux itérateurs [] et * et les domaines prédéfinis proposés par NewGen permettent de définir simplement toutes les structures de données.

Voici un exemple important: la représentation intermédiaire des programmes Fortran pour PIPS. La liste des domaines est donnée par ordre alphabétique; une présentation structurée en est faite dans la seconde partie. Il est recommandé d'avoir cet exemple à portée de main pour lire la suite de ce rapport.

array       = basic x dimensions:dimension* ;
basic       = int:int + float:int + logical:int + overloaded:unit + 
              complex:int + string:value ;
call        = function:entity x arguments:expression* ;
code        = declarations:entity* x statement ;
constant    = int + litteral:unit ;
dimension   = lower:expression x upper:expression ;
entity      = name:string x type x storage x initial:value ;
expression  = syntax ;
formal      = function:entity x offset:int ;
functional  = parameters:parameter* x result:type ;
instruction = block:statement* + test + loop + goto:statement + call ;
loop        = index:entity x range x body:statement x label:entity ;
mode        = value:unit + reference:unit ;
parameter   = type x mode ;
pgm         = modules:entity*
ram         = function:entity x section:entity x offset:int ;
range       = lower:expression x upper:expression x increment:expression ;
reference   = variable:entity x indices:expression* ;
statement   = label:entity x instruction ;
storage     = return:entity + ram + formal + rom:unit ;
symbolic    = expression x constant ;
syntax      = reference + range + call ;
test        = condition:expression x true:statement x false:statement ;
type        = statement:unit + area:int + array + functional + 
              unknown:unit + void:unit ;
value       = code + symbolic + constant + intrinsic:unit + unknown:unit ;

Certaines définitions sont simples à comprendre. Par exemple, une variable Fortran est représentée par un objet de type array, qui se compose d'un type de base basic et d'une liste de dimensions dimensions:dimension* (rappelons que basic est une abbréviation de basic:basic).

Un programme pgm se compose d'une liste modules de fonctions, chaque fonction étant représentée par un objet de type entity.

Le mode de passage des paramètres est un mode qui vaut soit value soit reference.

Implémentation C de NewGen

Nous allons à présent étudier les fonctions générées par NewGen-C, l'implémentation de NewGen pour le langage C. Nous ne décrirons pas NewGen-Lisp car cette seconde implémentation est tout à fait similaire.

Les fonctions que nous décrivons dans la suite sont générées par NewGen-C lors de la compilation d'un fichier de spécifications. Ces fonctions sont accessibles depuis un programme C à la condition d'inclure un fichier header nommé file.C_adt si file contient les spécifications². Il faut en outre utiliser une bibliothèque lors de l'édition de liens.

Définitions de types - Déclarations d'objets

Pour chaque domaine produit ou union dom, une directive typedef est générée. Ceci permet de déclarer très simplement des objets de type dom:

#include "ri.C_adt"
...
dom d ;                 /* declare une variable d de type dom */

extern dom f() ;        /* definit une fonction f renvoyant 
                           un objet de type dom */

Exemples:

dimension d ;
entity e;
extern constant EvalExpr() ;

Fonction de création - Domaines Produits

Une fonction de création make_dom est créée pour chaque domaine produit dom. Cette fonction prend autant d'arguments qu'il y a de sous-domaines dans la définition de dom; chaque argument est un objet du sous-domaine concerné que l'on veut stocker dans l'objet en cours de création. Les problèmes d'allocation mémoire sont gérés par Newgen-C.

Une valeur spéciale dom_undefined existe pour chaque domaine dom.

Exemples

d = make_dimension(l,u) ;
e = make_entity("+", type_undefined, storage_undefined, value_undefined) ;

Fonction de création - Domaine union

Une fonction de création make_dom est générée pour chaque domaine union dom. Cette fonction prend 2 arguments:

une étiquette de la forme is_dom_sdom qui indique à quel sous-domaine appartient l'objet s que l'on veut stocker dans l'objet nouvellement créé.
l'objet s appartenant à un des sous-domaines de dom, dont le type s'accorde avec l'étiquette is_dom_sdom décrite ci-dessus.

Les étiquettes is_dom_sdom sont automatiquement créées par NewGen-C.

Exemples:

syntax s = make_syntax(is_syntax_call, make_call(f, args)) ; 
value  v = make_value(is_value_constant, 
                      make_constant(is_constant_int, 3)) ;

Fonctions d'accès et de modification - Domaines produits

Si dom est un domaine produit, une fonction d'accès dom_sdom est créée pour chaque sous-domaine sdom de dom. Le type de cette fonction est celui du sous-domaine sdom. Appliquée à un objet d de type dom, elle retourne l'objet de type sdom stocké dans d.

Cette fonction est implémentée de telle sorte qu'elle puisse être utilisée en partie droite d'une affectation - pour accéder à la valeur du sous-domaine - ou en partie gauche - pour changer la valeur du sous-domaine.

Exemples:

constant c = EvalExpr(dimension_upper(d)) ;  
fprintf(fd, "%s" , entity_name(e)) ;
constant_int(value_constant(v)) += 1;

Fonctions d'accès - Domaines Unions

Soit dom un domaine union. L'accès à la valeur d'un sous-domaine stocké dans un objet d de type dom nécessite de connaıtre le type du sous-objet contenu dans d. La fonction or_tag permet de connaıtre ce type.

Par exemple, la fonction or_tag appliquée à l'objet v de type value créé auparavant fournit la valeur is_value_constant, c'est-à-dire la valeur de l'étiquette passée en paramètre au moment de la création de v.

Une fois le type connu grâce à la fonction or_tag la fonction d'accès dom_sdom peut être utilisée comme pour les domaines produits.

Exemple:

if (or_tag(v) == is_value_constant) {
        constant c = value_constant(v) ;
        if (or_tag(c) == is_constant_int) {
                int valeur = constant_int(c) ;
                ...
        }
        ...
}

Le prédicat dom_sdom_p(x) est équivalent à (or_tag(x)==is_dom_sdom) et est défini pour chaque sous-domaine sdom. Il permet de simplifier l'écriture des programmes.

Exemple:

        if(value_constant_p(v) ) {
                ....
        }

La fonction or_tag est néammoins utile pour l'instruction C switch.

Implémentation des listes

La liste vide est notée NIL. Les listes sont constituées à l'aide de cellules que nous nommons cons, par référence à Lisp. Une variable devant contenir une liste doit être déclarée de type cons *.

Un cons se compose d'un élément car permettant de stocker un objet d quel que soit le type de cet objet, et d'un élément cdr permettant de pointer vers une autre cellule cons.

Le type C de l'élément car est unique; appelons le chunk. Comme cet élément est susceptible de contenir un objet de n'importe quel domaine, une fonction d'insertion/extraction DOM est construite par NewGen-C pour chaque domaine dom. Cette macro permet de convertir un objet de type dom en un objet de type chunk, et réciproquement.

On ajoute un élément d de type dom à une liste l (l peut valoir NIL) grâce à la fonction CONS dont le type vaut cons* et qui prend 3 arguments:

la fonction de conversion DOM,
l'objet à insérer d de type dom,
la liste l.

La fonction CONS retourne en résultat la nouvelle liste, qui comporte l'élément en tête de liste.

Dans l'exemple suivant, f est une entity, e1 et e2 des expressions:

cons *la;

call c = make_call(f, NIL);
la = CONS(EXPRESSION , e1 , NIL) ;
call_arguments(c) = CONS(EXPRESSION , e2 , la) ;

La valeur de l'objet d de type dom contenu dans une cellule cons est obtenue par la fonction CAR dont le type est le type de l'élément car, c'est-à-dire chunk. Le résultat de CAR doit donc être converti en un objet de type dom grâce à la macro d'insertion-extraction DOM.

Exemple:

expression e = EXPRESSION(CAR(call_arguments(c))) ;

La cellule suivant une cellule cons s'obtient par la fonction CDR de type cons*. La fonction CDR peut être utilisée en partie gauche ou droite des affectations.

Exemple:

cons * pc ;
for (pc = call_arguments(c) ; pc != NIL ; pc = CDR(pc)) {
        constant c ;

        c = EvalExpression(EXPRESSION(CAR(pc))) ;
        ...
}

Implémentation des tableaux

L'accès à un élément d'un tableau se fait avec des []. Comme pour les listes, les objets d'un tableau sont stockés dans des éléments de type chunk. La macro d'insertion-extraction DOM doit donc encore être utilisée pour chaque accès au tableau.

Exemple: soit la spécification suivante:

#define N 10
system = a:int[N][N] x b:int[N] ;

Le domaine system s'utilise alors de la façon suivante:

main( )
{
   system s ;

   s = make_system(NIL, NIL) ;

   for (i = 0 ; i < 10 ; i++) {
      for (j = 0 ; j < 10 ; j++) {
         INT(system_a(s)[i][j]) = i*j;
      }
   }

   print_matrice(system_a(s)) ;
}

print_matrice(mat)
chunk mat[N][N] ;
{
   ...
}

Fonction d'Entrées-Sorties

Si d est un objet du domaine dom, d peut être écrit sur fichier par un appel à la fonction gen_write.

Cette fonction reconnaıt le type de d (dom) grâce à une information cachée dans d, et lui applique le traitement approprié. Chaque sous-domaine est écrit par un appel récursif à gen_write, le processus se terminant avec les domaines prédéfinis, pour lesquels la valeur est écrite. La fonction gen_write gère les listes et les tableaux.

Un objet écrit sur fichier par gen_write peut être lu par gen_read. Un appel à gen_read a pour effet de recréer un objet d' de type dom identique à l'objet initial d aux adresses mémoire près.

Il peut arriver que deux objets partagent le même espace mémoire, comme par exemple dans le cas d'un graphe dont deux noeuds ont un même successeur. On parle alors de sharing. Un autre cas de sharing arrive avec les listes circulaires, lorsque le dernier élément pointe vers le premier. Le sharing et les listes circulaires sont parfaitement gérés par gen_write et gen_read. L'objet recréé d' par gen_read comportera le même sharing et les mêmes listes circulaires que d.

Un objet peut être détruit par gen_free, fonction qui a le même comportement que gen_write: tous les sous-domaines sont récursivement détruits.

Exemple: le parseur de pips a un programme principal équivalent à:

{
        FILE * fd ;
        pgm p ;

        p = parse_program() ;

        fd  = fopen("exemple.rï, "w") ;
        gen_write(fd, p) ;
        gen_free(p) ;
}

Le paralléliseur a un programme principal équivalent à:

{
        FILE * fd ;
        pgm p ;

        fd  = fopen("exemple.rï, "r") ;
        pgm p = (pgm) gen_read(fd) ;
        pretty_print(parallelize_program(p)) ;
}

Lorsque tout marchera correctement, il sera possible de créer un unique programme pour économiser les accès au fichier fd:

pretty_print(parallelize_program(parse_program())) ;

Dans ce cas, les modifications à apporter aux programmes sont nulles.

Remarques sur l'implémentation

L'implémentation de NewGen-C est particulièrement efficace, et notamment:

les domaines pré-définis sont expansés dans les domaines produits et unions, dans les listes et dans les tableaux; il n'y a donc pas de gaspillage de mémoire ni d'indirection superflue;
par exemple, l'implémentation d'une liste d'entiers est conforme à ce que tout programmeur écrirait: chaque cons contient un entier et un pointeur sur le cons suivant;
la plupart des fonctions sont en fait des macros, d'où un gain en taille mémoire car il y a moins de fonctions, et un gain en rapidité;
les tests dynamiques de types et de cohérence des structures de données peuvent être inhibés pour améliorer la rapidité des parties du projet correctes.

Description de la représentation intermédiaire

Principe généraux

Cette représentation intermédiaire de programmes procéduraux a été définie pour traiter des programmes Fortran mais nous avons pris soin de nous appuyer sur les idées générales de la sémantique dénotationnelle pour obtenir une représentation à la fois concise, solide, extensible et aussi indépendante de Fortran que possible.

Cette représentation intermédiaire ne vise pas a rendre compte de tous les problèmes liés aux traitements interprocéduraux qui seront effectués dans le cadre du projet PIPS. Elle a pour but de représenter d'une manière sémantiquement équivalente un programme principal, une subroutine ou une function.

La conservation de la sémantique peut être estimée en essayant d'écrire un interpréteur Fortran basé sur cette représentation.

Il ne faut pas perdre de vue que cette représentation intermédiaire, comme toute structure de données, n'est que le squelette et que les procédures utilisant des informations issues d'elle ne verront en principe que la chair, c'est à dire les fonctions et procédures qui s'y appliqueront (évaluateur d'adresse, évaluateur d'expression, etc...) et qui utiliseront éventuellement d'autres structures de données privées.

Le présent document représente le résultat d'une première phase. La représentation intermédiaire sera ensuite augmentée pour prendre en compte les besoins de l'analyse interprocédurale ou du calcul des dépendances.

Spécification NewGen de la représentation intermédiaire

Le fichier de spécifications NewGen de la ri est donnée ci après. La liste définitions de domaines n'est pas donnée dans un ordre logique, mais plus simplement par ordre alphabétique.

array       = basic x dimensions:dimension* ;
basic       = int:int + float:int + logical:int + overloaded:unit + 
              complex:int + string:value ;
call        = function:entity x arguments:expression* ;
code        = declarations:entity* x statement ;
constant    = int + litteral:unit ;
dimension   = lower:expression x upper:expression ;
entity      = name:string x type x storage x initial:value ;
expression  = syntax ;
formal      = function:entity x offset:int ;
functional  = parameters:parameter* x result:type ;
instruction = block:statement* + test + loop + goto:statement + call ;
loop        = index:entity x range x body:statement x label:entity ;
mode        = value:unit + reference:unit ;
parameter   = type x mode ;
ram         = function:entity x section:entity x offset:int ;
range       = lower:expression x upper:expression x increment:expression ;
reference   = variable:entity x indices:expression* ;
statement   = label:entity x instruction ;
storage     = return:entity + ram + formal + rom:unit ;
symbolic    = expression x constant ;
syntax      = reference + range + call ;
test        = condition:expression x true:statement x false:statement ;
type        = statement:unit + area:int + array + functional + 
              unknown:unit + void:unit ;
value       = code + symbolic + constant + intrinsic:unit + unknown:unit ;

Analyse de la représentation intermédiaire

Dans cette section, nous allons montrer comment cette représentation intermédiaire permet de représenter les différents objets manipulés par un programme Fortran.

Domaines

Nous allons tout d'abord examiner chaque domaine pour expliquer brièvement à quoi il sert.

Entity = name:string x type x storage x initial:value

Tout objet ayant un nom dans un programme Fortran est représenté par une entity. Un tel objet peut être un module, une variable, un common, un opérateur, une constante, un label, etc. Pour chaque objet, le sous-domaine name de l'entité donne le nom de l'objet tel qu'il apparait dans le texte source du programme, le sous-domaine type donne le type de l'entité, le sous-domaine storage le genre d'allocation mémoire utilisé pour l'entité, et finalement, le sous-domaine initial donne la valeur initiale, si elle est connue, de l'entité. Le terme valeur initiale a ici un sens assez large, puisqu'il s'agit par exemple du code pour les entités représentant des modules.

Type = statement:unit + area:int + array + functional + unknown:unit + void:unit

Le domaine type représente le type d'une entité. Le sous-domaine statement est utilisé pour les labels d'instruction. Le sous-domaine area est utilisé pour les commons. Le sous-domaine array est utilisé pour toutes les variables, y compris les paramètres formels et le résultat d'une fonction. Le sous-domaine functional est utilisé pour les fonctions, pour les subroutines et pour le programme principal. Le sous-domaine void est utilisé pour le résultat d'une subroutine ou d'un programme principal.

Array = basic x dimensions:dimension*

Le domaine array représente le type d'une variable. Le sous-domaine basic donne le type Fortran de la variable. Le sous-domaine dimensions donne la liste des dimensions de la variable. Un scalaire est un tableau de zéro dimension.

Chaque dimension est une expression, qui n'est pas nécessairement constante dans le cas des tableaux formels. La constante prédéfinie de nom '*D*' est utilisée pour les tableaux de taille non définie (DIMENSION T(*)).

Basic = int:int + float:int + logical:int + overloaded:unit + complex:int + string:value

Le domaine basic permet de représenter un type Fortran tel que INTEGER ou REAL. La valeur de ce domaine donne la longueur en octets de la zone mémoire occuppée par une variable de ce type.

Dimension = lower:expression x upper:expression

Le domaine dimension permet de représenter une dimension d'un tableau, c'est à dire un couple borne inférieure - sous-domaine lower - borne supérieure - sous-domaine upper.

Functional = parameters:parameter* x result:type

Le domaine functional représente le type d'un module, c'est à dire une fonction, une subroutine ou un programme principal. Le sous-domaine parameters donne le type et le mode de passage de chaque paramètre, et le sous-domaine result donne le type du résultat. Ce dernier type vaut void pour les subroutines et les programmes principaux.

Parameter = type x mode

Le domaine parameter représente le type et le mode de passage d'un paramètre formel de module.

Mode = value:unit + reference:unit

Le domaine mode représente le mode de passage d'un paramètre formel de module. Le domaine contient un objet du domaine value pour le mode de passage par valeur et reference pour le passage par adresse.

Storage = return:entity + ram + formal + rom:unit

Le domaine storage permet de préciser dans quelle zone de la mémoire est stockée une entité. Il y a plusieurs zones, qui ne correspondent pas nécessairement à la réalité, c'est à dire aux zones de mémoire qui seraient affectées par un compilateur.

Le sous-domaine return permet de représenter les variables ayant pour nom le nom d'une fonction et auxquelles on affecte la valeur que la fonction doit retourner. L'entité pointée par return est la fonction concernée.

Le sous-domaine ram est reservé aux variables ayant une adresse en mémoire. Il permet de préciser dans quelle fonction et éventuellement dans quelle common ces variables ont été déclarées.

Le sous-domaine formal est réservé aux paramètres formels des modules.

Le sous-domaine rom est utilisé pour toutes les entités dont la valeur n'est pas modifiable, telles que les fonctions, les labels, les opérateurs, etc.

Ram = function:entity x section:entity x offset:int

Le domaine ram permet de préciser la déclaration d'une variable. Le sous-domaine function indique dans quel module une entité est déclarée. Le sous-domaine section indique dans quelle aire une entité est stockée; il y a une aire par common déclaré et deux aires spéciales nommées _STATIC et _DYNAMIC pour les entités locales. Enfin, le sous-domaine offset donne l'adresse dans l'aire de la variable.

Formal = function:entity x offset:int

Le domaine formal indique le module dans lequel un paramètre formel est déclaré grâce le sous-domaine function, et le rang de ce paramètre dans la liste des paramètres grâce au sous-domaine offset.

Value = code + instruction + symbolic + constant + intrinsic:unit + unknown:unit

Le domaine value permet de représenter les valeurs initiales des entités. Le sous-domaine code est utilisé pour les entités modules. Le sous-domaine symbolic est utilisé pour les entités constantes symboliques. Le sous-domaine constant est utilisé pour les entités constantes. Le sous-domaine intrinsic est utilisé pour toutes les entités qui ne dépendent que du langage, telles que les intrinsics Fortran, les opérateurs, les instructions, etc. Enfin le sous-domaine unknown est utilisé pour les valeurs initiales inconnues.

Symbolic = expression x constant

Le domaine symbolic est utilisé pour représenter la valeur initiale d'une entité constante symbolique, c'est à dire les PAAMETER de Fortran ou les CONST de Pascal. Le sous-domaine expression permet de stocker l'expression qui a permis d'évaluer la valeur initiale contenue dans le sous-domaine constant. Le sous-domaine expression n'est utile qui si on cherche à reproduire un texte source fidèle.

Constant = int + litteral:unit

Le domaine constant est utilisé pour représenter la valeur initiale des entités constantes. Seules les entités de type entier nous intéressent, ce qui explique qu'une constante puisse être soit un int soit un litteral dont on ne garde pas la valeur (type unit).

Code = declarations:entity* x statement

Le domaine code est utilisé pour stocker le corps des modules. Le sous-domaine declarations contient une liste d'entités qui sont les variables et commons déclarés dans la fonction. Le sous-domaine statement contient la séquence d'instructions du module.

Statement = label:entity x instruction

Le domaine statement permet de repérer les instructions d'un module. Le sous-domaine label contient une entité qui définit le label. Le sous-domaine instruction contient le corps de l'instruction.

Instruction = block:statement* + test + loop + goto:statement + call

Le domaine instruction permet de représenter les instructions d'un module. Une instruction peut être un sous-domaine block, c'est à dire une liste de statement, un sous-domaine test pour les instructions de test, un sous-domaine loop pour les boucles, un sous-domaine goto pour les goto qui contient le statement vers lequel le goto se branche, ou un sous-domaine call pour toutes les autres instructions: affectation, appel de subroutine, entrées-sorties, return, stop, etc. Toutes ces instructions sont représentées par des appels à des fonctions prédéfinies dont nous étudierons la nature plus loin.

Test = condition:expression x true:statement x false:statement

Le domaine test permet de représenter toutes les instructions à base de contrôle. Le sous-domaine condition contient l'expression à tester, et les deux sous-domaines true et false contiennent les instructions à exécuter selon la valeur du test.

Il faut noter que chaque instruction de contrôle de Fortran, à l'exception de l'instruction DO, est transformée en une combinaison sémantiquement équivalente de tests et de gotos.

Loop = index:entity x range x body:statement x label:entity

Le domaine loop permet de représenter les boucles du type DO Fortran ou FOR Pascal. Le sous-domaine index contient l'entité indice de boucle, le sous-domaine range contient les bornes de la boucle, le sous-domaine body contient le corps de la boucle, c'est à dire un statement, le sous-domaine label contient le label de fin de boucle, c'est à dire une entité.

Range = lower:expression x upper:expression x increment:expression

Le domaine range permet de représenter les bornes des boucles DO Fortran. Il y a trois sous-domaines lower, upper et increment de type expression qui sont respectivement la borne inférieure, la borne supérieure et l'incrément.

Call = function:entity x arguments:expression*

Le domaine call permet de représenter les appels de fonctions. Les fonctions jouent un rôle important dans notre représentation intermédiaire puisque les opérateurs et les instructions Fortran (READ, WRITE, RETURN, ...) sont représentées par des fonctions prédéfinies.

Le sous-domaine function est une entité qui définit la fonction appelée. Le sous-domaine arguments est une liste de sous-domaines expression qui représente les arguments d'appel de la fonction.

Expression = syntax

Le domaine expression permet de stocker les expressions. Pour l'instant, ce domaine ne se compose que d'un unique sous-domaine syntax, mais nous pensons ajouter ultérieurement d'autres sous-domaines, notamment pour conserver avec chaque expression linéaire un forme compilée, peut-être sous forme d'un vecteur.

Le sous-domaine syntax contient l'expression avec la même structure que celle du code source.

Syntax = reference + range + call

Le domaine syntax permet de représenter les expressions telles qu'elles apparaissent dans le texte source du programme. Un syntax est soit une reference à un élément de tableau (on rappelle que les scalaires sont des tableaux à 0 dimension) , soit un call à une fonction (les opérateurs sont représentés par des fonctions pré-définies), soit un range, dans le cas des expressions bornes de boucles.

Référence = variable:entity x indices:expression*

Le domaine reference est utilisé pour représenter une référence à un élément de tableau. Le sous-domaine variable contient une entité définissant la variable référencée. Le sous-domaine indices contient une liste expressions qui sont les indices de la référence.

Objets du langage Fortran

Nous montrons à présent comment les différents objets manipulés dans un programme Fortran sont traduits dans notre représentation intermédiaire.

Module

Un module est un programme principal, une fonction ou une subroutine.

Un module est représenté par une entity dont le name est le nom du module, le type est un functional qui indique le type des paramètres formels et du résultat, le storage vaut rom et le initial est un code qui contient le corps du module.

Les subroutines et le programme principal n'ont pas d'argument et retournent un void. Les noms des modules sont préfixés par des '_' et le nom du programme principal est prefixé par un '__' pour le différencier d'une subroutine.

Commons et aires

Une aire représente une partie de la mémoire où sont rangées les variables. Les commons sont des aires (voir plus loin).

Deux aires spéciales sont créées pour les variables qui n'appartiennent pas à un common (variables locales). Ces deux aires sont des entités qui ont pour name _STATIC et _DYNAMIC, pour type un area qui donne la longueur de l'aire, pour storage un rom et comme initial une value de type unknown.

L'appartenance d'une variable ou d'un common à l'une des ces deux aires spéciales indique si cette variable ou ce common est statique ou dynamique.

Un common est représenté par une entity dont le name est le nom du common, le type est un area qui donne la longueur du common en octets, le storage est un ram qui indique la fonction où le common est declaré (function) et l'aire où le common est rangé (section)..

Le nom des commons est préfixé par un '_', comme les autres identificateurs globaux.

Variables - Généralités

Les variables scalaires sont traitées comme des tableaux à 0 dimension.

Une variable est représentée par une entity dont le name est le nom de la variable.

Variables - Types

Le type d'une entité ``variable'' est un array qui donne le type fortran des éléments (basic), le nombre de dimensions (longueur de la liste dimensions) et les bornes de chaque dimension.

Variables - Allocation mémoire

Le storage d'une entité ``variable résultat de fonction'' est un return qui indique la fonction contenant cette variable.

Le storage d'une entité ``variable paramètre formel'' est un formal qui indique la fonction contenant ce paramètre et le rang de ce paramètre dans la liste des paramètres formels.

Le storage d'une entité ``variable locale ou globale'' est un ram qui indique dans quelle fonction la variable est déclarée (function), à quelle aire (common ou aire spéciale) elle appartient (section) et quelle est son adresse dans ce common (offset).

Variable - Valeur initiale

Le initial d'une entité ``variable'' vaut unknown sauf si cette variable est de type entier et est initialisée par data. Dans le cadre de la parallélisation, on ne s'intéresse pas aux autres variables.

Constantes numériques et symboliques

Les constantes sont considérées comme des fonctions. Elles sont donc représentées par des entités dont le name est le nom de la constante (12, 13.56E12, '*NOMBRE DE FACETTES:*', PI, MAXITER, etc.), dont le type est un functional à 0 paramètre et 1 résultat qui donne le type de la constante, dont le storage est un rom et dont le initial est un constant pour les constantes numériques et un symbolic pour les constantes symboliques.

Opérateurs

Les opérateurs Fortran sont considérés comme des fonctions. Ils sont donc représentés par des entités dont le name est le nom de l'opérateur, et dont le type est un functional qui indique l'arité de l'opérateur (longueur de la liste parameters) mais qui n'indique pas le type des paramètres ou du résultat car le sous-domaine basic vaut toujours overloaded. Le storage d'un opérateur est un rom et son initial un intrinsic.

Intrinsics

Les intrinsics Fortran (MAX, MIN, ABS, etc.) sont traités comme des opérateurs.

Labels

Les labels sont représentés par des entités dont le name est le nom du label préfixé par un '@', dont le type vaut statement, dont le storage vaut rom et dont le initial est une constante litterale.

Instructions simples

Les instructions simples de Fortran telles que RETURN, CONTINUE, STOP, READ, WRITE, PAUSE, END, ... sont considérées comme des fonctions intrinsèques. Elles sont donc représentées par des entités qui ont les mêmes caractéristiques qu'un opérateur à 0 paramètre. On ne tient pas a jour le nombre de paramètres car il ne sert à peu près à rien et que de toute façon, il est variable.

L'instruction PRINT est transformée en WRITE.

Instructions de contrôle

Toutes les instructions de contrôle du sous-Fortran que nous acceptons en entrée, à l'exception de l'instruction DO, sont transformées automatiquement en séquences équivalentes de tests à deux branches (une vraie et une fausse), de branchements inconditionnels et de boucles do.

      IF (I) 10, 20, 30

devient

      IF (I.LT.0) THEN
         GOTO 10
      ELSE
         IF (I.EQ.0) THEN
             GOTO 20
          ELSE
             GOTO 30
          ENDIF
      ENDIF

      IF (I.GT.J) I = I-J

devient

      IF (I.GT.J) THEN
         I=I-J
      ELSE
        CONTINUE
      ENDIF

Arguments des instructions d'entrées-sorties

Les arguments des instructions d'entrées-sorties sont soit des informations de contrôle (unité, format, longueur des enregistrements, etc.), soit des références à lire ou des expressions à écrire.

Dans notre représentation, les arguments des instructions d'entrées-sorties sont des listes de couples d'expressions. La première expression du couple est une constante chaine de caractères qui indique la nature de l'argument qui apparaissait dans l'instruction Fortran (UNIT=, FORMAT=, RECL=, ...). La seconde expression est la valeur de cet argument.

Le dernier couple de la liste d'un READ ou d'un WRITE n'est pas un vrai couple: le premier élément est une expression constante qui vaut IOLIST=, et le second élément est une liste d'expressions qui sont les références à lire ou les expressions à écrire.

Boucles implicites

Les boucles do implicites dans les entrées-sorties sont représentées par des appels à un opérateur prédéfini (en fait une fonction) de nom IMPLIED-DO, qui prend comme arguments une entité qui définit l'indice de la boucle, une expression range qui définit les bornes de la boucle, et une liste d'expressions.

Formats

Les formats sont conservés sous forme d'expressions constantes chaines de caractères. La constante de nom '*F*' est prédéfinie pour les formats libres (list-directed).

Voici un exemple d'instruction d'entrées-sorties.

      READ(2,'(5E16.6)') (IMD(I),I=1,NDOM), K

devient

      (READ 'FMT=' '(5E16.6)' 'UNIT=' 2 
            'IOLIST=' (IMPLIED-DO I 1,NDOM,1 IMD(I)) K)

Structures de données de l'analyse sémantique intraprocédurale

Le but de cette section est de présenter les structures de données utilisées pour implémenter les deux premières phases de la méthode d'analyse sémantique de Cousot et Halbwachs. Ces deux premières phases, traduction du graphe de contrôle en un système aux polyèdres et résolution de ce système, ont été introduites dans le précédent rapport intermédiaire.

Les ensembles de valeurs entières que peuvent prendre les variables scalaires entières des modules en chaque point de contrôle sont approximés par des polyèdres à bornes rationnelles et non entières pour diminuer la complexité des calculs.

Ces polyèdres peuvent être définis de deux manières équivalentes:

implicitement, par un système d'égalités et d'inegalités linéaires vérifié par les points appartenant au polyèdre,
ou explicitement, par un système générateur formé de sommets, rayons et droites dont les combinaisons linéaires sont les points du polyèdre.

Ces deux représentations, qui font l'objet des deux premières sous-sections, sont utilisées simultanément parce que certaines opérations s'effectuent mieux avec l'une qu'avec l'autre (intersection par système d'équations, union par système générateur) et parce qu'on les utilise toutes les deux pour éliminer la redondance qui apparaıt au fur et à mesure des calculs. Les polyèdres que nous manipulerons comporterons donc deux parties, l'une donnant la représentation par système d'équations et l'autre la représentation par système générateur.

La dernière sous-section est consacré à la représentation du système d'équations aux polyèdres construit à partir de la représentation intermédiaire produite par l'analyse syntaxique et à partir de son graphe de contrôle.

Représentation des systèmes d'égalités et d'inégalités linéaires

Le système de contraintes est représenté par la matrice de ses coefficients et par un vecteur de termes constants. Cette matrice, étant généralement très creuse, est représentée par des vecteurs creux et par lignes. En effet, il faut choisir entre une représentation par ligne et par colonne, et on effectue plus souvent des combinaisons linéaires de lignes dans l'algorithme de test de dépendance qui partage cette structure de données avec l'analyse sémantique.

Chaque colonne de la matrice correspond à une variable scalaire entière du module analysé, une entité de la représentation interne. Ces entités sont renommées 1, 2,... pour les traitements mathématiques mais on conserve un tableau de correspondance permettant de passer du numéro d'une variable à l'entité correspondante.

On complète chaque ligne de la matrice de contraintes par le terme constant qui reçoit conventionnellement le numéro de variable 0.

Vecteur

Un vecteur est une liste de couples (numéro de variable, valeur). Cette liste de couples n'est pas triée dans la première implémentation qui est faıte car nous faisons l'hypothèse que le nombre de coefficients non nuls restera très faible tout au long des calculs.

Le vecteur nul est représenté par une liste vide.

Ce type vecteur est utilisé pour représenter les contraintes, les sommets, les rayons et les droites.

Contrainte

Une contrainte est soit une égalité, soit une inégalité (on ne sait pas faire la distinction à ce niveau). Elle contient donc implicitement un terme constant associé à la variable de numéro 0.

On associe à chaque contrainte de type inégalité les éléments du système génerateur qui la sature au moyen de tableaux d'entiers.

Chaque contrainte contient aussi un pointeur vers une autre contrainte pour pouvoir constituer directement les deux listes d'égalités et d'inégalités d'un système.

Système

Un système linéaire est constitué de deux listes de contraintes, égalités et inégalités. C'est à ce niveau que l'on dispose de l'information n'ecessaire pour savoir comment traiter les termes constants. Il contient aussi le nombre de ces égalités et de ces inégalités, ainsi que le nombre de variables du système.

Pour permettre la sortie de messages compréhensifs, chaque système contient aussi un pointeur vers un tableau d'entiers permettant de retrouver les numéros d'entités correspondant à chacune de ses variables.

Représentation des systèmes générateurs

Définition d'un système générateur

Comme les systèmes générateurs sont moins connus que les systèmes d'inégalités, nous rappelons que ce sont des triplets de trois ensembles appelés respectivement sommets, rayons et droites. Le polyèdre généré par un système $S=\{\{\vec{s_i}\},\{\vec{r_j}\},\{\vec{d_k}\}\}$ est défini par l'équation:

$\begin{displaymath} P = \left\{ { \vec{v} / \exists \lambda_i \geq 0 \; \wedge... ... \sum_j \mu_j \vec{r_j} + \sum_k \nu_k \vec{d_k} }\right\} \end{displaymath}$

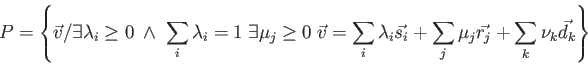
Sommets

Comme nous approximons les ensembles de valeurs entières par des ensembles de valeurs rationnelles, il se peut que les sommets aient des coordonnées rationnelles. Ils sont donc représentés par un vecteur à coefficients entiers et par un unique dénominateur.

On associe aussi à chaque sommet un tableau des équations qu'il sature (i.e. vérifie).

Enfin, chaque sommet contient un lien vers un sommet suivant, qui permet de constituer l'ensemble des sommets d'un système générateur.

Au plus haut niveau, on garde un pointeur vers le premier sommet, ainsi que le nombre total de sommets de la liste.

Rayons et droites

Les rayons et les droites sont des objets identiques. Seule change l'interprétation qu'on en donne et la manière dont on les traite.

Ils sont représentés comme les sommets, mais ne contiennent pas de champs dénominateur puisqu'ils sont définis à une constante multiplicative près. A chacun d'eux est associé un vecteur, un ensemble de numéro d'équations saturées, et un pointeur vers l'élément suivant. En tête de liste, on conserve le nombre d'éléments.

Système générateur

Un système générateur comporte donc trois champs, qui sont les têtes de liste des sommets, des rayons et des droites.

Représentation d'un système d'équations aux polyèdres

Un système d'équations aux polyèdres est une structure de données complexe qui mérite une description en plusieurs étapes.

Représentation d'un polyèdre

Un polyèdre est représenté par une paire de pointeurs, un vers le système générateur du polyèdre, l'autre vers son système d'inégalités et égalités.

Le système

Un système d'équations aux polyèdres comprend quatre champs. Le premier champ permet de passer des numéros de variables propres aux routines mathématiques aux numéros d'entité définis par l'analyseur syntaxique.

Le second champs permet de connaıtre le nombre des variables effectivement utilisées dans l'analyse sémantique. Le troisième champ est le système d'inégalités qui définit l'état initial du module.

Enfin le quatrième champ est composé d'une liste généralisée d'équations sémantiques. Les éléments primitifs sont les équations sémantiques, mais les équations relatives aux instructions d'un corps de boucle sont regroupées en une sous-liste, et ce, récursivement.

Cette structuration hiérarchique des équations, qui reflète la structure du graphe de contrôle, permettra de rechercher d'abord les points fixes du système sur les boucles les plus internes.

Equation sémantique

Une équation sémantique a cinq champs. Le premier est le polyèdre caractérisant les valeurs des variables en ce point du programme. Le second donne la liste des paramètres permettant de calculer en fonction des autres polyèdres et le troisième le type de relation existant entre et les . Le quatrième champ permet de savoir si ce polyèdre doit être conservé ou non pour être ultérieurement utilisé dans le processus de parallélisation. Le cinquième et dernier champ permet de savoir à quel point de contrôle du module il faut rattacher l'information .

Divers types d'équations sémantiques

Les différents types d'équations que nous savons traiter sont:

les affectations non-linéaires (
les affectations linéaires inversibles (
les affectations linéaires non-inversibles (
les tests non linéaires,
les tests linéaires de type inégalité pour les branches vrai et faux (
les tests linéaires à égalité, branches vrai et faux (
les noeuds de jonction qui sont les noeuds du graphe de contrôle qui ont plus d'un antécédent (regroupement après un ou en tête de d'un
les noeuds d'élargissements, qui caractérisent les boucles et qui permettent d'éviter les itérations infinies vers un point fixe (opérateur d'élargisssement défini par Cousot).

A chaque type d'équations est associé une structure de données différentes dont les champs contiennent exactement les paramètres nécessaires: polyèdre(s) en entrée, variable modifiée, expression linéaire, etc...

Conclusion

Les structures de données présentées dans ce rapport d'avancement numéro 2 permettent de construire les premiers programmes du projet PIPS. Notons que celles qui sont relatives à l'analyse sémantique seront probablement modifiées pour diminuer le temps d'exécution, qui est le talon d'Achille de la méthode d'analyse de Cousot et d'Halbwachs.

Footnotes

... rapport ¹: Ce rapport est en cours d'étude par l'équipe de Pierre Leca, à l'O.N.E.R.A.
... spécifications ²: si l'ordre import est utilisé, il faut inclure plusieurs fichiers header; la liste des fichiers à inclure et l'ordre dans lequel ils doivent être inclus sont donnés par NewGen-C au moment de la compilation.

Document Actions

Send this

Mo	Tu	We	Th	Fr	Sa	Su
				1	2	3
4	5	6	7	8	9	10
11	12	13	14	15	16	17
18	19	20	21	22	23	24
25	26	27	28	29	30

RAPPORT D'AVANCEMENT No 2 ANALYSE SYNTAXIQUE ET SEMANTIQUE RT EMP 105

RAPPORT D'AVANCEMENT No 2 ANALYSE SYNTAXIQUE ET SEMANTIQUE RT EMP 105

Footnotes

This Site Uses Cookies

RAPPORT D'AVANCEMENT No 2
ANALYSE SYNTAXIQUE ET SEMANTIQUE
RT EMP 105